In this ongoing series, we ask SF/F authors to describe a specialty in their lives that has nothing (or very little) to do with writing. Join us as we discover what draws authors to their various hobbies, how they fit into their daily lives, and how and they inform the author’s literary identity!
The ancient art of paper-folding (zhezhi in Chinese and origami in Japanese) can be impressive to viewers of all ages.
But no less impressive is the mathematics behind origami. The origamist-mathematician may be unique in exploring a contemporary branch of mathematics that is as tangible and physical as the geometry of the ancient Greeks.
As anyone who has folded a paper crane knows, there is a unique pleasure in working with a flat sheet of paper and through folding, creasing, tucking, and other manipulation, transforming it into something quite magical. The material, at once pliant and rigid, allows the mind to reason with abstract geometry in a way that cannot be replicated through other means.

The wonders of mathematical origami can be easily seen in its application. Origami-derived techniques have been used in the design of solar panels for spacecraft because they allow large structures to be folded up into a compact form for launch; and then, once in space, the structures can unfold in a simple, reliable way with little need for assembly or human intervention.
In 1995, a Japanese satellite, the Space Flyer Unit, used a technique called the Miura fold to deploy its solar panels. Named after the Japanese astrophysicist Koryo Miura, this folding technique creases the flat surface into a tessellation of parallelograms that can be easily pulled apart and collapsed. You can learn to do the Miura fold yourself by following the directions in this paper by Yutaka Nishiyama. The resulting sheet can be collapsed or expanded simply by pulling on opposite corners.

The technique is a little tricky to master, and it took a while before robots could do the folding well enough that we can now get subway maps folded in this space-age manner. And it turns out that nature already uses a version of Miura folding: researchers at the Centre for Biomimetics, University of Reading, discovered that the furled leaves of beech and hornbeam trees unfold from the bud in a similar manner as the origami pattern.
Origami has also proven to be a fruitful avenue of research for metamaterials—materials engineered to have specific properties derived from their structure by assembling elements in some repeating pattern. In the case of metamaterials based on the Miura fold, for example, it’s possible to “program” the rigidity and compressibility of the material by selectively inverting the “peaks” formed in the tessellation with a pattern of “pop-through defects” (PTDs).
Video illustrating pop-through defects in Miura-fold material. Reproduced from J. L. Silverberg, A. A. Evans, Lauren McLeod, Ryan Hayward, Thomas Hull, Christian D. Santangelo, I. Cohen (2014, August). “Using origami design principles to fold reprogrammable mechanical metamaterials,” Science, 345, 647-650. Used with permission.
It’s easy to get a feel for origami-mathematics for yourself. One of the first books to explore the mathematics behind paper folding in the West is T. Sundara Row’s Geometrical Exercises in Paper Folding, published in Madras, India in 1893. Among other topics, this book examines how, using only a sheet of paper and only straight folds, it’s possible to construct squares, equilateral triangles, pentagons, hexagons, octagons, and other polygons; to illustrate the progression of arithmetic series and the summation of the geometric series in Zeno’s Paradox of Achilles and the Tortoise; to prove the Pythagorean Theorem and derive algebraic formulas; and even to explore conic sections.
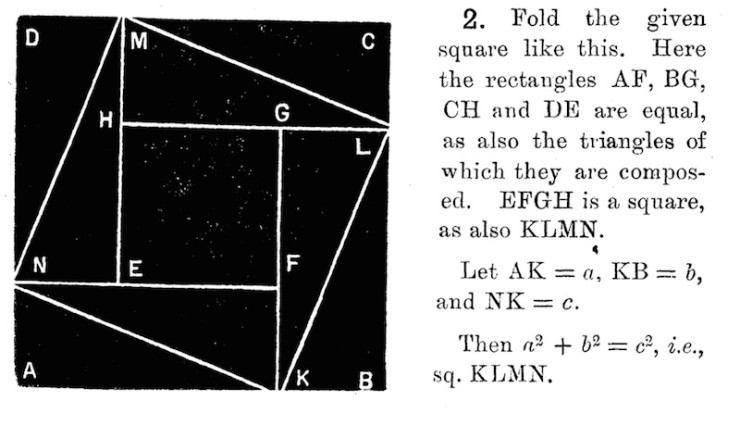
In the book’s introduction, Row explains that he was inspired by a kindergarten exercise to use paper folding as a means to explore geometry:
It would be perfectly legitimate to require pupils to fold the diagrams on paper. This would give them neat and accurate figures, and impress the truth of the propositions forcibly on their minds … [W]hat is now realized by the imagination and idealization of clumsy figures can be seen in the concrete.
Introduction, Geometrical Exercises in Paper Folding
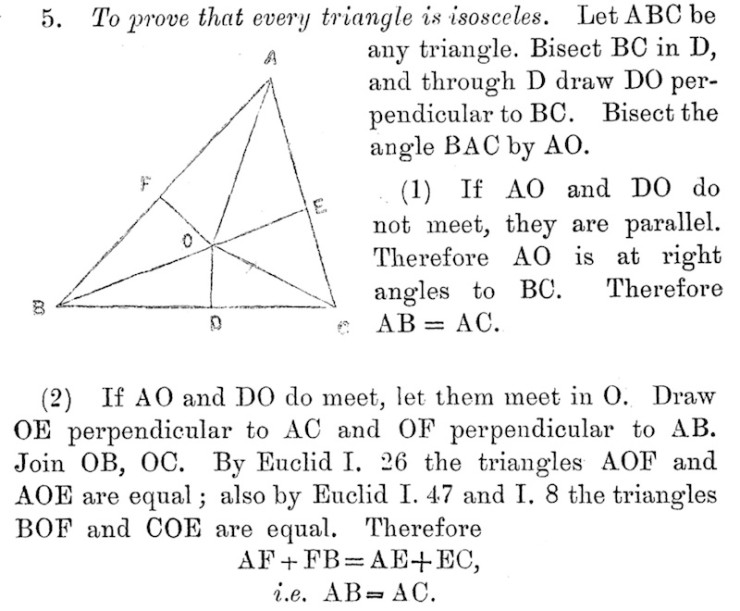
Row then proceeds to show the following (fallacious) proof for the proposition that “every triangle is isosceles”:
Like Row, I invite the reader to try to crease a triangular piece of paper to form the lines AO and DO, which will reveal the fallacy in a most interesting manner.
Folding and creasing paper to construct geometric figures probably reminds you of constructions done with the compass and straightedge in the manner of Euclid. As it turns out, paper-folding is actually more powerful than compass and straightedge, and is capable of constructions such as trisecting an angle or doubling a cube, feats impossible with Euclid’s tools. (One wonders how the history of mathematics would have developed had Euclid been an origamist—that might make an interesting SF story…)
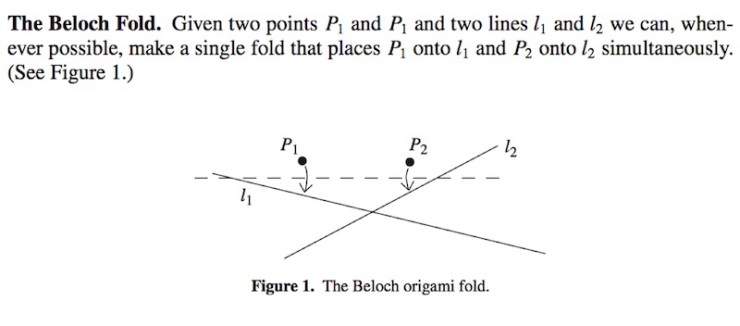
This is largely due to the ability for paper folders to employ a “Beloch fold,” which is a single fold that maps two points on the paper to two lines on the paper. The Beloch fold is named after Margherita Piazzola Beloch, an Italian mathematician who contributed to the mathematics of paper folding as well as photogrammetry—the art of taking measurements from photographs. (The complete set of folds that can be made from a single sheet by a paper-folder are described by a set called the Huzita-Hatori axioms. The “Beloch fold” corresponds to Axiom 6.)
Figure reproduced from Thomas C. Hull (2011, April). “Solving Cubics With Creases: the Work of Beloch and Lill.” The American Mathematical Monthly, 118, 307-315. Used with permission.
Essentially, the Beloch fold is equivalent to finding the common tangent to two parabolas, which also suggests that this fold is equivalent to solving a cubic equation. Since the compass and straightedge are capable only of solving quadratic equations, this is how paper-folding gets its extra power. (For a detailed visual explanation and proof, consult the Hull paper linked above.)
Just as paper folding in the past allowed practitioners to extract the mathematical principles behind the art, the rigorous application of mathematical reasoning has in turn given contemporary paper-folders the ability to create precise, elaborate geometric constructions. We are living, in many ways, in the golden age of paper folding, with ever more inventive and interesting models being devised.
As a writer and reader, the pleasure of origami reminds me a great deal of the pleasure of reading and writing speculative fiction. Just as origami allows the mind to manipulate concrete shapes instead of the “idealization of clumsy figures,” speculative fiction, by literalizing what is otherwise metaphorical, allows us to experience the abstract and the intangible via manipulatives.
And so we can measure our humanity via a Voigt-Kampff machine, affirm our mettle by summoning corporeal Patronuses, scrutinize historiography through an alternate United States, evaluate our emotional responses to political fables on a battlestar, and admire the love of a mother in a menagerie of animals made of paper.
Ken Liu is the author of The Paper Menagerie and Other Stories. To learn more about the book, look here.